|
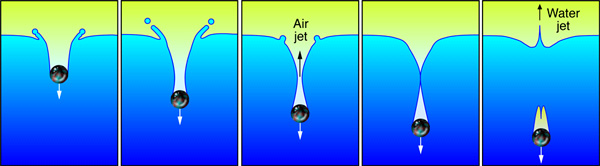
Столкновение твердого тела с ровной поверхностью жидкости рождает последовательность нетривиальных событий, являющихся предметом активного интереса ученых на протяжении уже более ста лет. В 1908 году была издана книга «Splash of a drop» английского физика Артура Уортингтона. В своей книге он впервые подробно исследовал и описал процесс столкновения твердого тела с жидкой средой. Если попытаться кратко изложить это явление, происходит следующее (см. рис. 1): сталкивающийся объект образует в жидкой среде полость с вертикальной осью симметрии, которая, благодаря гидростатическому давлению, начинает схлопываться, что приводит к образованию воздушного перешейка (или сужения) и в конечном итоге — к отсечке стенками жидкости воздушной полости. Далее из точки, где воздушная полость отсекается, выбрасываются вверх и вниз две очень тонкие струи — струи Уортингтона.
Год назад «Элементы» рассказывали о публикации группы голландских и испанских физиков, построивших по результатам своих экспериментов теоретическую модель, объясняющую экстремально малую толщину струй Уортингтона. Теперь эта же коллаборация обнаружила необычный эффект, который возникает при падении тела в жидкость. Оказывается, схлопывающаяся воздушная полость создает струю воздуха, которая имеет скорость, близкую к скорости звука. Более того, в самый последний момент, перед тем как воздушная полость отсекается жидкостью, скорость вытекающего из нее воздуха значительно превосходит даже скорость звука, то есть исходящий из полости поток воздуха становится сверхзвуковым. Результаты своих экспериментальных и теоретических исследований ученые опубликовали в статье Supersonic Air Flow due to Solid-Liquid Impact в журнале Physical Review Letters (полный текст доступен здесь, PDF, 472 Кб).
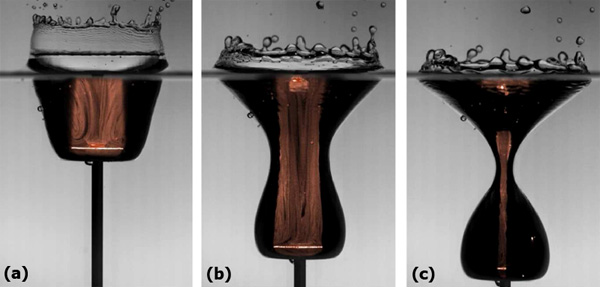
Экспериментальная установка состояла из тонкого круглого диска радиусом 2 см. К центральной части его нижней стороны был прикреплен тонкий стержень, с помощью которого имитировалось падение диска с постоянной скоростью 1 м/с. Чтобы визуализировать, как воздух вытекает из образующейся воздушной полости, ученые использовали микроскопические (3 мкм) капельки глицерина. Эти капельки создавали над поверхностью воды дымовую завесу, которая затем увлекалась диском при его вхождении в жидкость. В распоряжении исследователей также находилась высокоскоростная камера, способная записывать видео со скоростью 15 000 кадров в секунду. На рис. 2 показаны три снимка, полученные с помощью такой камеры.
|
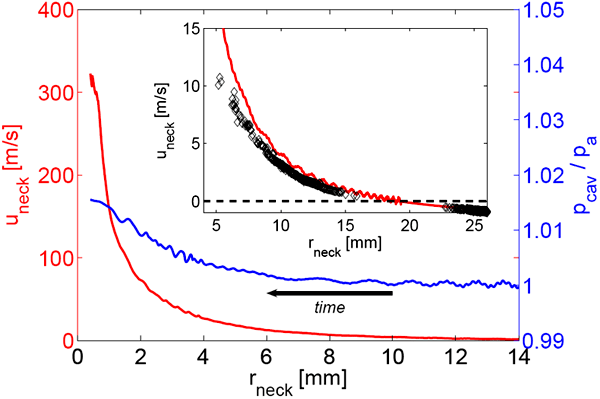
Поскольку технология, используемая авторами статьи, не позволяла им измерить скорость струи воздуха при дальнейшем сближении водяных стенок полости, они прибегли к численному моделированию динамики воздушного потока с помощью уравнений Эйлера. Графики на рис. 3 иллюстрируют результаты их расчетов, а именно — зависимости давления внутри воздушной полости pcav и скорости воздушной струи uneck, текущей через перешеек полости, от его радиуса rneck. Из графиков следует, что, когда радиус перешейка составляет около 0,5 мм, скорость струи через сужение достигает 330 м/с, то есть скорости звука. Такая скорость струи возникает за счет того, что давление воздуха внутри полости на 0,02 атмосферы больше окружающего. Удивительно, но такой небольшой разницы давлений оказалось достаточно, чтобы заставить воздух двигаться через сужение со скоростью звука.
|
Чтобы удостовериться в правильности своих вычислений, ученые на теоретическую кривую зависимости uneck от rneck наложили аналогичную экспериментальную зависимость (вставка на рис. 3). Явное согласие экспериментально полученных точек (черные ромбы) и сплошной теоретической кривой (красного цвета) указывало, по мнению ученых, на правильность их теоретической модели.
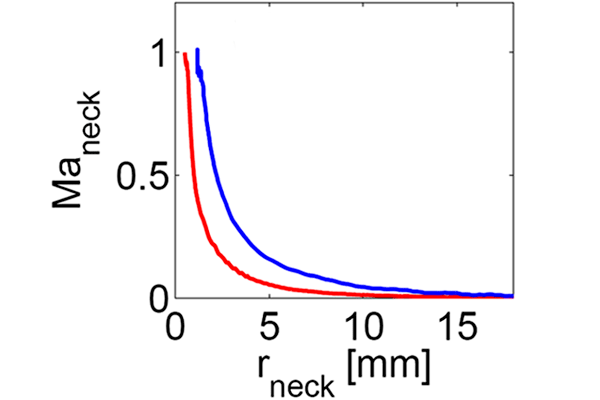
Далее авторы статьи решили определить более точно радиус перешейка, при котором воздух начинает течь через него со звуковой скоростью. Для этого они рассчитали эволюцию числа Маха (отношение скорости воздушной струи через сужение к скорости звука) в зависимости от радиуса перешейка для скорости диска 1 и 2 м/с (рис. 4).
|
Выяснилось, что, как только радиус перешейка уменьшается до 0,5 мм для меньшей скорости и 1,2 мм для большей, число Маха равно 1 — что означает, что воздух протекает через перешеек со скоростью звука.
Однако в названии обсуждаемой статьи употребляется выражение «сверхзвуковое течение воздуха» (supersonic air flow). Возникает вопрос: так где же в полости воздух течет со сверхзвуковой скоростью?
Если внимательно присмотреться к графикам на рисунках 3 и 4, можно увидеть, что расчетные кривые заканчиваются, когда радиус перешейка составляет 0,5 мм (для скорости диска 1 м/с), что соответствует скорости воздушного потока приблизительно 330 м/с. Дальнейший численный анализ установил, что скорость больше скорости звука воздушная струя приобретает, как только она миновала перешеек.
|
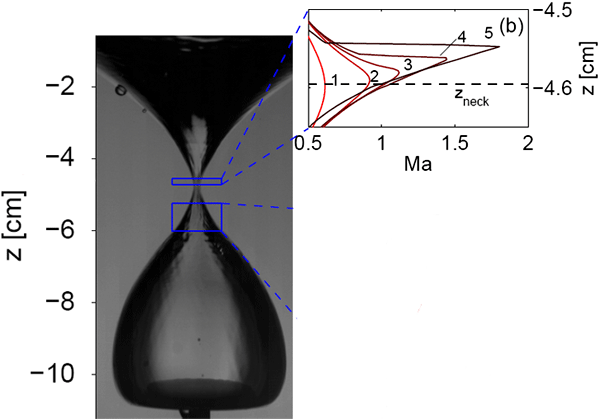
На рис. 5 показано распределение чисел Маха (Ma) воздушной струи вдоль вертикальной оси симметрии полости на участке, ограниченном верхним синим прямоугольником, когда радиус перешейка менялся от 0,9 мм (кривая 1) до 0,5 мм (кривая 5). Легко видеть, что максимальное значение Ма для области воздушного потока, расположенной чуть выше перешейка с радиусом 0,5 мм (местоположение перешейка на графике указано пунктирной линией) равно 1,75 (кривая 5). Вспомнив определение числа Маха, несложно посчитать, что струя воздуха в этот момент и в этой области двигается со скоростью почти 580 м/с.
Таким образом, сверхзвуковое течение воздуха, согласно численному моделированию, должно наблюдаться в узкой области сразу над перешейком буквально перед самым его исчезновением. Такое поведение воздушной полости в воде напоминает сопло Лаваля — специальную конструкцию, предназначенную для ускорения проходящего через него газового потока до сверхзвуковых скоростей.