Экспериментально подтверждено существование сверхпроводимости полуторного рода

Диборид магния MgB₂ содержит сразу два вида куперовских пар, одни из которых соответствуют сверхпроводимости первого, а другие — второго рода. Группе физиков из Бельгии и Швейцарии удалось показать, что в слабом магнитном поле MgB₂ ведет себя не так, как другие сверхпроводники: решетка пронизывающих его магнитных вихрей оказалась неоднородной. Такую сверхпроводимость предложено называть сверхпроводимостью «1,5-го рода».

Когда говорят о сверхпроводнике, в первую очередь интересуются его критической температурой Т_с — температурой перехода из сверхпроводящего состояния в нормальное. Однако для сверхпроводника не менее важны и следующие характеристики: ?₀ — глубина проникновения магнитного поля; ?₀ — длина когерентности и ?₀ — энергетическая щель. (Индекс 0 у этих величин означает, что их значения берутся при абсолютном нуле температур — при Т = 0 К.) Чтобы дальнейшее изложение было понятным, нам придется сначала описать физическое содержание этих трех параметров, а также рассмотреть разницу между сверхпроводниками первого и второго рода.

Лондоновская глубина, длина когерентности, энергетическая щель

Сверхпроводимость — это не только нулевое электрическое сопротивление материала, но и его идеальный диамагнетизм, выражающийся в эффекте Мейснера—Оксенфельда: сверхпроводник не пропускает внутрь себя внешнее магнитное поле, экранируя его токами в очень тонком приповерхностном слое. Глубина этого слоя при Т = 0 обозначается как ?₀. Т. е. хотя поле всё же проникает в сверхпроводящий материал, оно очень быстро, экспоненциальным образом, в нём затухает — так что на глубине более ?₀ от поверхности сверхпроводник уже можно считать идеальным диамагнетиком. Параметр ?₀ часто называют лондоновской глубиной проникновения магнитного поля (London penetration depth) — по имени братьев Лондонов (Fritz and Heinz London), которые математически описали эффект Мейснера—Оксенфельда. По мере приближения температуры к критической глубина проникновения в сверхпроводник внешнего поля (с фиксированным значением индукции) растет. При Т = Т_с внешнее магнитное поле захватывает материал полностью. Подробнее о механизме проникновения внешнего поля в сверхпроводник мы расскажем чуть позже.

Чтобы понять, что такое длина когерентности, вспомним, что сверхпроводник представляет собой «резервуар» коллективизированных электронов проводимости, объединенных в пары (называемые куперовскими) и текущих без трения как единое целое сквозь кристаллическую решетку материала. Грубо говоря, расстояние между электронами в такой паре и есть длина когерентности ?. Она, как и лондоновская глубина проникновения, зависит от температуры: с возрастанием температуры расстояние между электронами в куперовской паре увеличивается. При приближении температуры к критической это расстояние стремится к бесконечности, что означает температурное разрушение куперовской пары, а в макроскопическом масштабе — переход материала в нормальное (не сверхпроводящее) состояние.

Разрушить куперовскую пару можно не только путем повышения температуры, но и прикладывая к ней энергию — например, облучая инфракрасным светом. Энергия связи такой пары электронов (при нулевой температуре) равна 2?₀ — удвоенное значение энергетической щели. С ростом температуры ? (уже без индекса 0) уменьшается — до нуля по достижении Т_с.

В 1957 году А. А. Абрикосов сформулировал критерий деления сверхпроводников на две группы, введя отношение ? = ?₀/?₀. Если ? первого рода, в противном случае (когда ? > 1/v2) — второго рода. К сверхпроводникам первого рода относятся все чистые элементы, за исключением ванадия и ниобия. Сверхпроводящие сплавы, интерметаллические соединения и т. п. вкупе с ванадием и ниобием — сверхпроводники второго рода. C экспериментальной точки зрения это разделение определяет поведение сверхпроводников в магнитном поле и механизм проникновения в них поля.

Сверхпроводники 1-го рода

Внешнее магнитное поле, индукция которого не превышает критического значения В_с, не проникает в сверхпроводник первого рода, оставляя вещество сверхпроводящим. Когда В достигает B_c, силовые линии пронизывают сверхпроводник, переводя его в нормальное состояние.

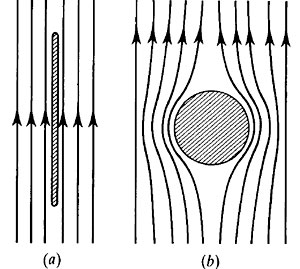
Однако такая картина перехода вещества из сверхпроводящего в нормальное состояние несколько идеализирована. Она будет наблюдаться, только если в нашем распоряжении находится тонкая пластина или длинный цилиндр, а внешнее поле прикладывается параллельно ее (его) оси, см. рис. 1а. В реальности образец не всегда пластина или цилиндр, да и магнитное поле может прикладываться «неправильно». Например, на рисунке 1b видно, что плотность силовых линий у экватора шара больше, чем у полюсов, а это означает, что и поле там сильнее. Поэтому может случиться так, что значение В внешнего поля будет несколько меньше В_с, но за счет локального уплотнения силовых линий вблизи экватора индукция превысит критическое значение и сверхпроводимость исчезнет, в результате чего в экваториальной области шара образуется резистивный участок.

Состояние в сверхпроводнике 1-го рода, когда сверхпроводящие домены соседствуют в материале с нормальными областями, называется промежуточным. Такое состояние может возникать при значениях индукции приложенного поля, лежащих в интервале (1–D)B_c B B_c, где размагничивающий фактор D определяется формой образца. Интервал изменения размагничивающего фактора — от нуля (для длинного цилиндра или тонкой пластины в параллельном поле) до единицы (для плоскопараллельной пластины в случае, когда поле приложено перпендикулярно ее поверхности). Для шара значение D составляет 1/3; для цилиндра в поле, перпендикулярном его оси, — 1/2.

Проникновение магнитного поля в сверхпроводник происходит в виде вихревых «ниток». Каждая такая нитка имеет вытянутое вдоль направления магнитного поля нормальное (т. е. не сверхпроводящее) ядро цилиндрической формы с диаметром порядка длины когерентности ?. Через это ядро проходит магнитное поле — поэтому вокруг него возникает кольцо незатухающих вихревых токов (с шириной, приблизительно равной лондоновской глубине ?).

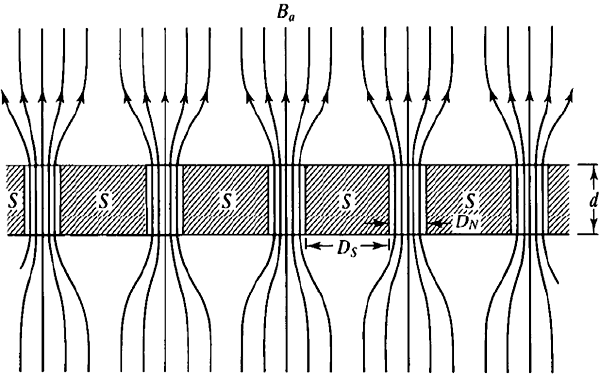
Одна вихревая нитка в сверхпроводнике 1-го рода может включать большое количество флюксоидов (fluxoids, fluxons) — квантов магнитного потока, каждый из которых несет в себе поток ?₀ = 2,068·10^–15 Вб (вебер). Вихри притягиваются друг к другу, и чем меньше расстояние между ними, тем сильнее притяжение. За счет этого они «слипаются», образуя вышеупомянутые нормальные домены (см. рис. 2) — макроскопических размеров и не обязательно цилиндрической формы.

Сверхпроводники 2-го рода

В сверхпроводники 2-го рода магнитное поле также проникает в виде вихревых «ниток». Но есть существенные отличия от сверхпроводников 1-го рода.

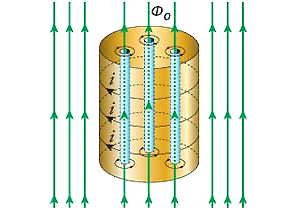
Первое: каждый вихрь несет в себе только один флюксоид (см. рис. 3). Второе: вихри отталкиваются друг от друга (чем ближе, тем сильнее), образуя т. н. вихревую треугольную решетку, которую еще называют абрикосовской (соответственно, и вихри получили имя абрикосовских). И третье: у сверхпроводников 2-го рода критических значений индукции внешнего поля два. Проникновение вихрей происходит тогда, когда значение индукции магнитного поля заключено в диапазоне (1–D)В_c1 В В_c2.

При В = В_c1(1–D) вихри начинают проникать в материал, а когда В достигает второй критической величины, В_c2 (которая может быть во много раз больше, чем В_c1), они полностью заполняют сверхпроводник, переводя его в нормальное состояние. Важно понимать, что, несмотря на наличие абрикосовских вихрей, в интервале (1–D)В_c1 В В_c2 вещество по-прежнему сверхпроводящее, хоть и содержит нормальные области. Такое состояние сверхпроводника 2-го рода называется смешанным.

Отметим, что вихревая решетка — не абстракция, а эффект, реально наблюдаемый в магнитном поле при помощи различных экспериментальных методик: см. галерею изображений абрикосовских решеток на сайте Лаборатории сверхпроводников Университета Осло.

Сверхпроводники «полуторного» рода

В 2001 году была открыта сверхпроводимость в дибориде магния, характеризующаяся аномально высокой критической температурой — около 39 К. Как выяснилось, в MgB₂ существует сразу два «сорта» куперовских пар (и, соответственно, две энергетические щели), которые взаимодействуют между собой и за счет этого создают столь высокую критическую температуру.

Каждой из двух энергетических щелей ?₁ и ?₂ соответствует своя длина когерентности ?₁, ?₂ и лондоновская глубина проникновения ?₁, ?₂. Если применить критерий Абрикосова для MgB₂, то получится, что для первой щели ? = ?₁/?₁ ? 0,66 , а для второй — ? = ?₂/?₂ ? 3,68 > 1/v2. Получается, что в дибориде магния одновременно «живут» две сверхпроводимости — первого и второго рода.

Поскольку сверхпроводники 1-го и 2-го рода различаются характером проникновения магнитного поля в вещество, хорошо было бы узнать, каким образом поглощает магнитное поле двухзонный сверхпроводник с куперовскими парами обоих «родов». И вот здесь всё оказалось не вполне однозначным.

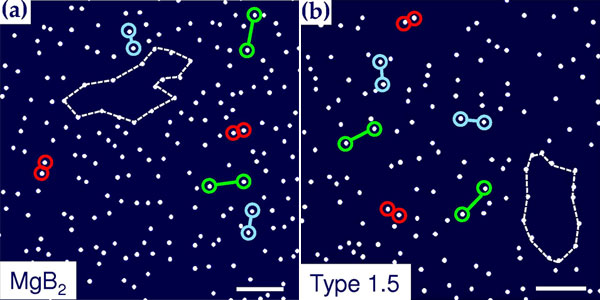
В 2003 году в журнале Physical Review B появилась статья ученых из России, Швейцарии и США Vortex structure in MgB₂ single crystals observed by the Bitter decoration technique, в которой они сообщали о наблюдении абрикосовской решетки в чистом монокристалле MgB₂ в слабом магнитном поле. Эксперимент показал, что диборид магния, несмотря на наличие в нём двух энергетических щелей, можно отнести к сверхпроводникам второго рода. Результат подтверждался снимком треугольной вихревой решетки (рис. 4). Вихри распределены равномерно — что, по мнению исследователей, доказывает факт наличия в MgB₂ сверхпроводимости второго рода.

Однако недавно группа исследователей из Бельгии и Швейцарии опубликовала в Архиве препринтов результаты своего эксперимента под говорящим заголовком «Сверхпроводники 1,5-го рода» (Type-1.5 Superconductors). Во внешнем магнитном поле напряженностью 1 эрстед (в 4 раза слабее, чем в эксперименте 2003 года) они получили для сверхпроводящего чистого монокристалла диборида магния необычную картину вихревой решетки — с неравномерным распределением вихрей, см. рис. 5а. Эта нерегулярность связана с тем, что, как предсказывает теория, взаимодействие магнитных вихрей должно напоминать поведение межмолекулярных сил: на близких расстояниях вихревые структуры отталкиваются, на далеких — начинают притягиваться. Такое поведение вихрей авторы статьи считают главной особенностью сверхпроводимости «полуторного» рода.

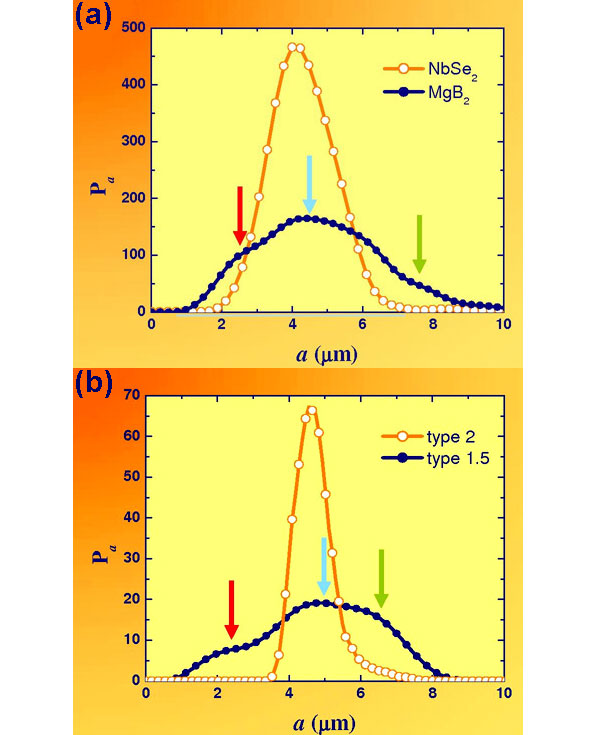
Чтобы не быть голословными, ученые количественно оценили обнаруженную неоднородность. Они применили для экспериментальных снимков, визуализирующих вихревые решетки диборида магния и диселенида ниобия NbSe₂ (сверхпроводник 2-го рода), триангуляцию Делоне и рассчитали распределение расстояний между соседними вихрями; результаты см. на рис. 6а. На рис. 6b — аналогичные данные, полученные в результате численного моделирования на основе теоретических расчетов для сверхпроводников второго и «полуторного» рода.

Распределение расстояний между соседними вихрями для NbSe₂ (оранжевая кривая на левом графике) — гауссово. Единственный пик показывает, что расстояние между соседними вихрями в большинстве случаев близко к постоянному и составляет около 4 мкм; это и означает, что вихри распределены равномерно.

Аналогичное распределение для диборида магния (темно-синяя кривая на левом графике) — не только не гауссово, но и имеет три пика, отмеченные стрелками; т. е. расстояние от какого-либо заданного вихря до его ближайшего соседа с большой вероятностью составляет либо 2,5, либо 4,5, либо 7,5 мкм; таким образом, в этом случае распределение вихрей действительно нерегулярное. По мнению исследователей, вихревая решетка в MgB₂ напоминает паутину; они назвали такую структуру «паутинной» (gossamer).

Очень похожие кривые распределения получаются, и если провести теоретический расчет вихревой структуры для обычного однозонного сверхпроводника 2-го рода и для двухзонной сверхпроводимости — иными словами, для сверхпроводника 1,5 рода (см. рис. 6b). Имеем «однопиковую», т. е. однородную структуру вихревой решетки для сверхпроводника второго рода и «трехпиковую», а значит, неоднородную, — для сверхпроводника 1,5 рода. Сравнивая рисунки 6a и 6b, нетрудно заметить хорошее согласие между экспериментальными и теоретическими данными.

Поле напряженностью 1 эрстед (с индукцией 0,0001 тесла) — очень слабое. Дальнейшее увеличение напряженности, как показали эксперименты с MgB₂ во внешнем поле 5 эрстед, радикально меняет вихревую решетку сверхпроводника полуторного рода: полосы с высокой и низкой плотностью вихрей чередуются (как белые и черные полоски у зебры). Если же поле увеличить до 10 эрстед, то различия в вихревых решетках между диборидом магния и диселенидом ниобия исчезают: вихри распределяются равномерно. В этом нет ничего удивительного — такое поведение сверхпроводника 1,5 рода теория также предсказывает.

У читателя может возникнуть вопрос: почему же такую структуру вихревой решетки диборида магния не наблюдали еще тогда, в 2003 году? По мнению авторов обсуждаемой работы, причина в том, что снимок вихревой решетки был получен для очень небольшой области образца (приблизительно 10 на 10 микрон), где неоднородность могла просто в достаточной мере не проявиться. К тому же вырастить идеально чистый кристалл MgB₂ очень непросто, а любые примеси могут радикальным образом исказить картину.

По мнению ученых, «паутинную» вихревую решетку можно будет наблюдать и у других двухзонных сверхпроводников — в частности, недавно открытых сверхпроводящих соединений на основе железа, например Ba_0,6K_0,4Fe₂As₂.

Похожие статьи: