|
В вопросе происхождения жизни современная биология придерживается идеи абиогенеза — возникновения жизни из неживой материи благодаря эволюции взаимодействующих химических соединений в исходном «бульоне». Естественно, процесс этот был не одномоментным, а состоял из большого числа этапов. Некоторые из них уже были воспроизведены лабораторно (скажем, синтез некоторых аминокислот из простейшей органики, создание молекул-репликаторов, способных катализировать сборку своих копий, и т. п.), но, несмотря на все усилия, до восстановления полной цепочки еще очень далеко.
Вопрос о самых первых этапах возникновения жизни относится скорее к химии, нежели к биологии. Более того, на него можно даже взглянуть с точки зрения теоретической химфизики. Вместо простого перебора всевозможных смесей простейших реагентов и условий, в которых они находятся, можно задаться вопросом: какими общими закономерностями должны обладать нужные химические реакции безотносительно к конкретным молекулам? Скажем, естественно ожидать, что при абиогенезе уже на самых ранних этапах должны в зачаточном виде проявляться основные свойства живого: способность к размножению, способность к закреплению мутаций, различная для разных мутаций скорость размножения в заданных внешних условиях. Однако эти требования дарвиновской эволюции сформулированы на «биологическом» языке, и совершенно не очевидно, как их перевести на язык химических реакций и какие реакции будут ими обладать.
Именно эти вопросы изучались в статье Marginally stable chemical systems as precursors of life, опубликованной недавно в журнале Physical Review Letters. В ходе теоретического анализа на стыке химической термодинамики и математики автор пришел к любопытному выводу: «эволюция» может спонтанно возникать за счет термодинамических флуктуаций в химических реакциях с безразличным равновесием.
Механическое и химическое равновесие
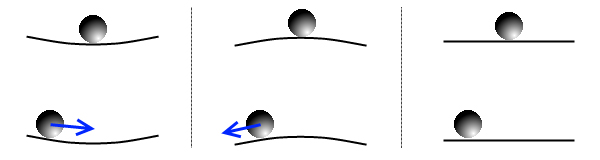
Ключевыми в этой формулировке являются слова «безразличное равновесие». И прежде чем рассказывать о самой работе, полезно на простейшем механическом примере напомнить, какие вообще бывают типы равновесия. На рис. 1 показан шарик на вогнутом, выпуклом и ровном столе. Шарик, лежащий в углублении (рис. 1, слева), находится в состоянии устойчивого равновесия: если шарик чуть-чуть сдвинуть, возникнут силы, которые будут стремиться вернуть его в исходное положение. Шарик, аккуратно поставленный на вершину холма (рис. 1, в центре), находится в неустойчивом равновесии: любое, сколь угодно малое внешнее воздействие (например, удар одной молекулы воздуха) будет стремиться увести его прочь. Наконец, положение равновесие шарика на абсолютно горизонтальном столе (рис. 1, справа) называется безразличным — при смещении шарика не возникает никаких сил, тянущих его обратно или уводящих прочь.
У безразличного равновесия есть две отличительные особенности. Во-первых, таких точек равновесия должно быть бесконечно много, в противовес всего одной точке устойчивого или неустойчивого равновесия. Это правило действует и в обратную сторону: если мы обнаружили, что в какой-то системе есть бесконечный непрерывный набор положений равновесия, то значит, эти равновесия безразличные. Во-вторых, если на систему (в нашем случае, на шарик) в дополнение ко всему действует какая-то посторонняя сила, пусть даже очень слабая, она может заставить шарик «путешествовать» по всем возможным положениям равновесия — опять же, в отличие от (не)устойчивого равновесия, где эта сила ни на что не влияет. Поэтому при изучении систем с безразличным равновесием надо всегда быть начеку: любое слабое воздействие, которым мы пренебрегли бы для (не)устойчивого равновесия, тут может сильно изменить ситуацию.
Интересно теперь представить себе, как химические реакции выглядят с этой точки зрения. Возьмем стандартную картинку: смесь веществ поместили в нужные условия, началась химическая реакция и, исчерпав весь запас реагентов, остановилась. Это справедливо в случае ограниченного запаса реагентов; если же химическая реакция идет при постоянном притоке исходных реагентов и оттоке ее продуктов, процесс выйдет на стационарный режим: концентрация реагентов и продуктов реакции достигнет некоторого значения и перестанет зависеть от времени. Этот режим можно называть динамическим равновесием: реакция протекает, но только ее эффект в точности компенсируется притоком и оттоком веществ.
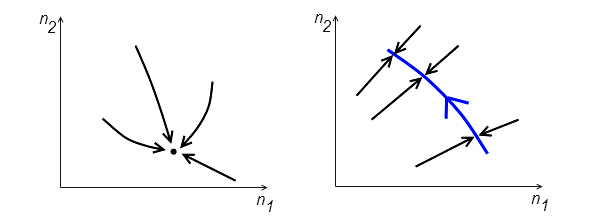
Ход такой химической реакции можно наглядно изобразить на диаграмме, по осям которой показаны концентрации каких-либо веществ, участвующих в реакции (см. рис. 2). Каждая точка на диаграмме отвечает некоторой пропорции этих веществ. Если эта пропорция меняется с течением времени (например, когда реакция только-только «разгорается»), соответствующая точка будет двигаться по диаграмме. Стационарный же режим отвечает неподвижной точке химического равновесия.
|
В подавляющем большинстве случаев это равновесие устойчиво. Это значит, что если в ходе такой реакции изменить баланс реагентов, уведя тем самым систему из положения равновесия, то химические реакции быстро вернут ее в исходное состояние (рис. 2, слева). Существуют, впрочем, реакции, в которых концентрации веществ не фиксированы, а изменяются периодически во времени. На диаграмме такая реакция будет отвечать не точке, а циклу, однако этот цикл тоже устойчив — при смещении с цикла реакция адаптируется так, чтобы вернуться на него.
Однако, по аналогии с механической системой, можно представить себе химические реакции и с безразличным положением равновесия. Выглядеть они будут так, как схематично показано на рис. 2, справа. Если реакцию запустить из какой-то начальной точки, то соотношение веществ придет к одному из многочисленных равновесных значений — реакция быстро «сядет» на линию положений равновесия. В этом случае у системы появляется «эффект памяти»: конкретное положение химического равновесия зависит от начальных условий.
Равновесие в автокаталитических реакциях
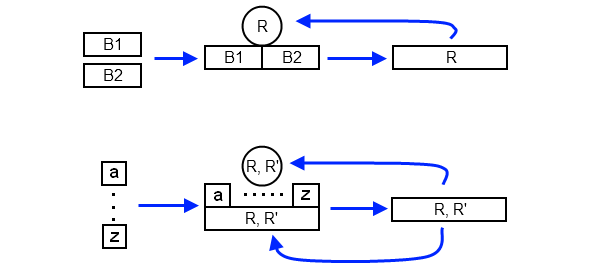
Эти более или менее абстрактные рассуждения можно теперь применить к ключевым для абиогенеза автокаталитическим реакциям, в которых некоторые молекулы катализируют создание своих собственных копий. Простейшая автокаталитическая реакция заключается в следующем: некоторая молекула R собирает из простых молекул-субстратов свою копию, которая тут же включается в работу и катализирует сборку следующих копий себя (рис. 3, вверху). Но в такой реакции нет шансов на эволюцию. Если в силу каких-то причин молекула R мутировала в R', она либо не сможет уже выполнять исходную задачу, либо сможет, но при этом будет снова воспроизводиться исходная молекула R. Никакой возможности спонтанно перенастроиться на производство R' в такой схеме нет. Иными словами, если в такой реакции некоторые молекулы R превратились в R' (систему вывели из положения равновесия), то они уже не будут «размножаться», а значит, их доля будет неуклонно стремиться к нулю. Такая реакция демонстрирует устойчивое равновесие, которое не позволяет закрепиться мутациям молекулы R, поскольку они не наследуются.
|
Иная картина возникает, если R выполняет функцию настоящей репликазы — то есть катализирует сборку не какой-то одной жестко заданной молекулы, а молекулы, соответствующей произвольной матрице (например, достраивает комплементарную цепочку по произвольной цепочке РНК). Здесь в качестве матрицы может выступать в том числе и сама молекула R, а также ее мутантные формы (рис. 3, внизу). Даже если мутантная форма репликазы, R', неактивна (то есть она сама не может уже ничего катализировать), то она всё равно размножается под действием R. Если же репликаза-мутант сохраняет свою функцию, то она тоже включается в цикл и может катализировать сборку как R, так и R'. Иными словами, мутации не устраняются, а продолжают жить и размножаться.
Как показал автор обсуждаемой статьи, именно в таких автокаталитических реакциях и возникает безразличное химическое равновесие. Он построил математическую модель описанной выше ситуации, принял во внимание разную степень «активности» молекул R и R' и проанализировал, к каким пропорциям концентраций R и R' будет стремиться химическая реакция. Оказалось, что таких точек равновесия бесконечное число, и они образуют кривую, как на рис. 2, справа. Именно безразличное равновесие, то есть нежелание системы стремиться к какой-то одной точке на диаграмме, позволяет благополучно сосуществовать разным вариантам одной молекулы в более или менее произвольной пропорции.
А теперь самый любопытный факт: в такой системе сама собой появляется медленная направленная эволюция дарвиновского типа. Весь предыдущий анализ относился к тому «рафинированному» случаю, когда концентрация всех молекул R и R' была одинакова во всём пространстве. В реальности, конечно, всегда имеются какие-то неоднородности. Даже если реагенты полностью перемешаны, всегда есть термодинамические флуктуации — случайные отклонения количества молекул от среднего в любом объеме. В результате в каждом микроскопическом объеме смеси раз за разом возникают новые условия (неравновесные концентрации), и реакция постоянно пытается адаптироваться к этим смещениям из положения равновесия.
С помощью численного моделирования автор работы проанализировал суммарный эффект от таких флуктуаций. Он обнаружил, что из-за них состояние химического равновесия всей системы в целом начинало медленно ползти вдоль линии положений равновесия в сторону доминирования более активной версии репликазы. Этот «дрейф» показан синей стрелкой на рис. 2, справа. Иными словами, система эволюционировала; «выгодная» мутация репликазы не просто выживала, но и мало-помалу начинала преобладать. Важным свойством этой эволюции является то, что она протекает довольно медленно и требует больших объемов воды, поскольку чем больше объем, тем более сильные отклонения в нём могут возникнуть. Возвращаясь к самому первому механическому примеру, можно сказать, что «термодинамический шум» оказался той самой слабенькой силой, которая была неважна для устойчивого равновесия, но которая начала управлять движением системы с безразличным равновесием.
Итак, теоретический анализ показал, что в принципе возможны химические реакции с участием молекул-репликаторов, обладающие безразличными равновесиями, в которых сама собой возникает направленная эволюция в сторону более эффективного репликатора. Однако отсюда до нахождения реальной цепочки, приведшей к той жизни, которую мы знаем, еще далеко. Прежде всего, химикам вообще пока неизвестны примеры реакций с безразличным равновесием. Может быть, они плохо искали; может быть, такие реакции требуют слишком тонкой «подстройки» или даже запрещены какими-то законами — это еще предстоит выяснить. Никаких конкретных примеров автор обсуждаемой статьи не приводил, поскольку его задача состояла лишь в изучении того, что в принципе разрешено химической кинетикой. Поэтому экспериментальная демонстрация таких реакций станет первым шагом на пути к реализации этой идеи о начальных этапах возникновения жизни.