|
Что такое сопротивление?
Всем известно, что электрический ток в веществе — это направленное движение свободных заряженных частиц. В металле ток создается свободными электронами — электронами, находящимися на самых далеких орбитах атома и слабо связанными с атомным ядром. Чтобы возникло направленное движение, необходимо на концах проводника создать разность потенциалов или напряжение. Вызванное напряжением электрическое поле в металле заставляет электроны диффундировать в нём. Движущиеся заряженные частицы сталкиваются, теряют часть своей энергии и рассеиваются на ионах, различных дефектах, неоднородностях кристаллической решетки и примесях в веществе. Такое диссипативное (то есть сопровождающееся уменьшением энергии) рассеяние и приводит к возникновению сопротивления.
Если электроны рассматривать как частицы, подчиняющиеся в своем движении классическим законам физики, то, записав второй закон Ньютона, можно получить математическую взаимосвязь между плотностью тока, идущего через металл, и электрическим напряжением, вызывающим его протекание. Проще говоря, можно теоретически вывести экспериментальный закон Ома. Именно так в начале XX века Пауль Друде получил теорию электронной проводимости металлов и, в частности, знаменитую формулу для сопротивления, названную его именем (см. Теория Друде). Одними из главных характеристик в теории Друде были длина и время свободного пробега электронов в металле между столкновениями с «помехами». Поскольку формула Друде неплохо описывала сопротивление проводников, то она практически не изменилась даже тогда, когда появилась квантовая механика.
В 70-е годы было открыто отрицательное магнитосопротивление — уменьшение сопротивления проводника при увеличении индукции магнитного поля. Это открытие никак не укладывалась в рамки теории Друде. В 1979 году американские и советские физики установили, что к классической формуле сопротивления необходимо добавить слагаемое, связанное с квантовым поведением электрона, поскольку электрон, согласно известному принципу дуализма, не только частица, но и волна. Иными словами, сопротивление надо объяснять не только столкновением частиц, но и учитывать так называемые эффекты квантовой интерференции электронных волн.
Через год Борис Альтшулер с коллегами построил количественную теорию этого явления, объяснившую, в частности, отрицательное магнитосопротивление. В их статье, помимо уже известных классических величин, таких как время и длина свободного пробега электронов, появились новые характеристики для описания сопротивления — время и длина фазовой когерентности электронов. Длина фазовой когерентности — это расстояние бездиссипативного рассеяния электрона, то есть дистанция, которую преодолевает электронная волна или электрон, не испытав неупругого рассеяния (не утратив первоначальную энергию). Время фазовой когерентности — это время между неупругими столкновениями электрона, или время, в течение которого электронная волна не теряет свою энергию. Из определения следует, что на такой длине электрон дает нулевой вклад в общее сопротивление металла.
Понижение температуры подавляет вероятность неупругого столкновения электронной волны и, соответственно, вероятность уменьшения энергии электрона, отражающегося на макроскопическом уровне в виде снижения сопротивления. Следовательно, чем меньше температура, тем больше время и длина фазовой когерентности. Например, при температуре жидкого гелия (около 4 К) масштаб фазовой когерентности составляет примерно один микрометр для многих металлов.
У читателя может возникнуть вопрос: так чем же друдевская длина свободного пробега электрона отличается от длины фазовой когерентности, которая на первый взгляд имеет такой же физический смысл? Всё дело в том, что в классической теории совершенно не важно, упруго или нет электрон сталкивается с ионом, дефектом и т. п. Любое рассеяние электрона трактуется как событие, приводящее к увеличению сопротивления вещества. При квантовом подходе электроны в пределах длины фазовой когерентности упруго сталкиваются с препятствиями на своем пути и не меняют свою энергию до некоторого момента, пока вероятность неупругого столкновения с помехой не станет значительной.
Персистентные токи и причины их возникновения
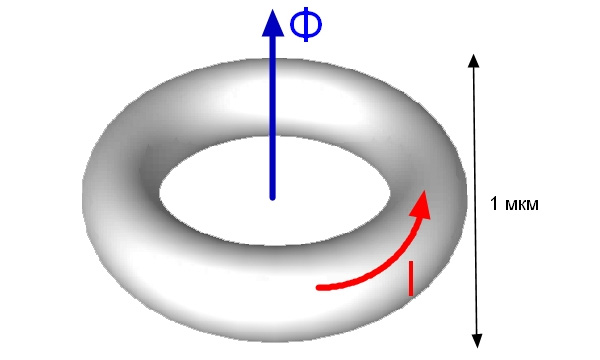
На квантовые поправки к сопротивлению в 1983 году обратили внимание физики Рольф Ландауэр, Маркус Бюттикер и Йозеф Имри, опубликовавшие в журнале Physics Letters A интересную гипотезу. Что будет, если взять металлическую проволоку с длиной и площадью поперечного сечения меньшей или равной длине фазовой когерентности, замкнуть ее в кольцо, охладить до низких температур и потом пронизать магнитным потоком (рис. 1)?
Ученые пришли к выводу, что в таком кольце начнут течь незатухающие токи, не имеющие ничего общего с токами в сверхпроводниках. Их назвали персистентными токами (от англ. persistent «постоянный»). Магнитное поле здесь играет важную роль. Дело в том, что электроны с равной вероятностью двигаются в кольце либо по часовой стрелке, либо против, то есть в среднем ток в кольце равен нулю. Разрушить эту симметрию и задать конкретное направление движению электронов — главная задача магнитного поля.
Заметим, что различия между сверхпроводящими и персистентными токами весьма существенны. Как уже было сказано, электрон может двигаться без сопротивления в пределах длины фазовой когерентности. В сверхпроводнике за счет объединения электронов в пары, а точнее, в куперовские пары, их длина и время фазовой когерентности равны бесконечности. Они перемещаются без сопротивления сколь угодно долго и на сколь угодно большое расстояние. Более того, сверхпроводящий ток создают абсолютно все электроны проводимости металла.
В случае с персистентным током никакого объединения частиц в пары не происходит. Персистентный ток создают лишь те электроны, для которых существует наибольшая вероятность беспрепятственного перемещения в пределах длины фазовой когерентности. Некоторые частицы даже в пределах фазовой когерентности не в состоянии двигаться без потерь своей энергии. Понижая температуру, мы не только увеличиваем длину фазовой когерентности, но и увеличиваем вероятность бездиссипативного прохождения через препятствия для большего количества электронов. Однако всё равно остаются частицы, для которых эта задача непреодолима.
Описанное явление кажется невероятным, но давайте вспомним, что движение электрона вокруг атомного ядра тоже можно интерпретировать как незатухающий ток. Грубо говоря, аналогичная картина наблюдается и в металлическом кольце.
На макроскопическом уровне разница между этими двумя видами токов проявляется в том, что величина текущего персистентного тока не зависит от площади поперечного сечения кольца. Более того, сверхпроводящий ток в кольце с такими же размерами будет намного больше персистентного тока в нём. Интересно отметить здесь еще и тот факт, что персистентный ток существует в кольце, которое фактически обладает сопротивлением. Ничто не мешает подключить к кольцу источник питания и тем самым заставить течь по нему ток. Просто общий ток будет суммой или разностью обычного тока, идущего от батарейки, и персистентного тока (всё зависит от направления протекания обычного тока).
Чудеса на этом не заканчиваются. Теоретики, помимо всего прочего, показали, что значение персистентного тока осциллирует в зависимости от магнитного потока, пронизывающего кольцо. Период таких колебаний равен отношению двух фундаментальных констант — постоянной Планка h и заряда электрона e (h/e = 4,1·10–15 Тл·м2). В физике отношение h/e называют квантом магнитного потока — флюксоидом (в сверхпроводимости флюксоид в 2 раза меньше: h/2e; двойка возникает из-за объединения электронов в куперовские пары). Максимальное значение персистентного тока (максимальная амплитуда) будет наблюдаться, когда магнитный поток через кольцо составляет целое число флюксоидов. Если же магнитный поток кратен половине флюксоида, то персистентный ток не возникнет.
Несмотря на то что причины возникновения персистентных токов уже не подвергаются сомнению, теория этих токов до конца пока что так и не построена. Во-первых, нет четкой формулы, определяющей величину персистентного тока в кольце. Во-вторых, хотя и ясно, что направление протекания тока зависит от количества электронов, участвующего в этом движении, теоретики не могут точно предсказать, в какую сторону он потечет. Всё основывается лишь на приблизительных оценках. Так, для температуры 1 К в кольце диаметром около 1 мкм (это соответствует длине фазовой когерентности при температуре 1 К) амплитуда персистентного тока должна иметь значение порядка одного наноампера (10–9 А).
К настоящему времени выдвинуто несколько правдоподобных теоретических моделей, описывающих данный эффект. Каждая из них предсказывает периодичность по магнитному потоку и каждая дает результаты, совпадающие по порядку величины с вышеприведенным 10–9 А. Но все модели сильно различаются в числе перед степенью 10–9. Поэтому узнать, какая из теорий количественно верно описывает явление персистентного тока, можно лишь проведя эксперименты по наиболее точному измерению его величины.
Хотелось бы подчеркнуть, что причины, вызывающие возникновение персистентных токов, имеют исключительно квантовую природу. Это относится и к магнитному потоку, пронизывающему кольцо. «Классическое» влияние магнитного поля в виде силы Лоренца, действующей на все движущиеся заряженные частицы, несущественно. Не вдаваясь в подробности, приведем такой наглядный пример. Пусть магнитный поток через кольцо диаметром порядка 1 мкм создается с помощью длинного соленоида диаметром, скажем, 0,5 мкм. Его расположение таково, что плоскость кольца перпендикулярна оси соленоида и пересекает его середину. За пределами соленоида индукция равна нулю, и магнитное поле фактически не влияет на кольцо. Так было бы в классической физике. Однако согласно квантовой механике, динамика электронов обусловлена не индукцией поля, а его так называемым векторным потенциалом, который вне соленоида нулю никак не равен. Вообще говоря, описанная здесь ситуация известна в физике как пример проявления эффекта Ааронова–Бома. Таким образом, можно сказать, что появление персистентных токов в кольце обусловлено двумя причинами — фазовой когерентностью электронов и эффектом Ааронова–Бома.
Эксперименты по наблюдению и измерению персистентных токов
В первой части новости было сказано, что при очень низкой температуре длина фазовой когерентности равна приблизительно 1 мкм. Значит, изготовив кольцо с длиной окружности около микрометра и охладив его до гелиевых температур, можно наблюдать и измерять незатухающий персистентный ток.
Однако, как это часто бывает, возникли проблемы технического плана. Прежде всего, металл не должен быть сверхпроводящим при низкой температуре. Такие материалы есть — это золото, медь и серебро, — так что в принципе вопрос с материалом решается. Другая проблема — в невозможности непосредственно впаять в кольцо амперметр, да еще и микроскопических размеров, чтобы измерить персистентный ток. Таких амперметров просто нет, да и сила тока настолько мала (около 1 нА), что находится вне измерительного диапазона самых точных измерительных приборов такого класса. Тогда ученые пошли другим путем. Измерить возникающий незатухающий ток можно посредством специальных, очень чувствительных магнитометров — СКВИДов (SQUID). По зарегистрированной величине магнитного поля, создаваемого персистентными токами, затем легко восстановить значение тока, соответствующее наблюдаемому полю.
Используя эту методику, группа ученых из Белловской лаборатории во главе с Лораном Леви — спустя 7 лет после выхода в свет работы Бюттикера, Ландауэра и Имри — провела в 1990 году первый эксперимент по наблюдению и измерению персистентных токов на массиве (около 100 тыс. штук) небольших, приблизительно 0,5 мкм в диаметре, медных колец (см. L. P. Levy, G. Dolan, J. Dunsmuir, H. Bouchiat. Magnetization of mesoscopic copper rings: Evidence for persistent currents // Phys. Rev. Lett. 64, 2074–2077). Результат оказался неутешительным: персистентные токи есть, они действительно зависят от магнитного потока через кольца, и их величина осциллирует с периодом равным одному флюксоиду. Но точно измерить их величину оказалось не под силу даже СКВИДу — чувствительность магнитометра группы Леви была на уровне измеряемой величины. К тому же возникали сильные помехи из-за магнитных примесей в веществе, всегда присутствующих даже в очень чистом кольце.
Позже были предприняты новые попытки, под руководством других ученых, измерить персистентные токи с помощью всё тех же СКВИДов, однако во всех экспериментах разброс данных был так велик, что часто разнился на порядки. Единственным достижением было подтверждение наличия колебаний тока с периодом h/e. Стало ясно, что инструментальная погрешность существующих магнитометров не позволяет точно измерить наблюдаемый эффект.
И вот недавно в журнале Science появилась совместная статья американских и немецких ученых Persistent Currents in Normal Metal Rings, оригинальным образом исследовавших персистентные токи в массивах алюминиевых колец с диаметром около 1 мкм. Предложенная ими конструкция позволяет измерить величину персистентных токов с беспрецедентной точностью — в 250 раз точнее, чем это удавалось с помощью СКВИД-магнитометров. Впервые точность измерения персистентных токов оказалась достаточной для проверки правильности существующих теоретических моделей.
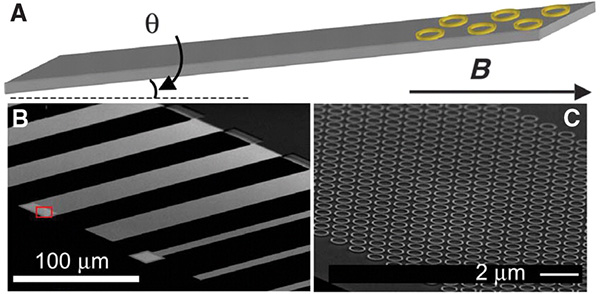
Экспериментальная установка авторов статьи представляла собой кремниевую пластину — кантилевер, — на которой литографическим образом (см. Электронная литография) было нанесено 1680 колец с одинаковых диаметром 308 нм (рис. 2). Вся система охлаждалась до температуры ниже 1 К и помещалась в магнитное поле порядка 1 Тл (такая огромная величина магнитной индукции не позволяла кольцам переходить в сверхпроводящее состояние при данной температуре, несмотря на то что алюминий становится сверхпроводником уже при 1,2 К).
|
Пластина располагалась под некоторым углом по отношению к силовым линиям магнитного поля. Компонента магнитного поля, перпендикулярная пластине, индуцировала персистентный ток. Одновременно с этим параллельная составляющая придавала кантилеверу вращательный момент. Сам по себе вращательный момент есть произведение нескольких величин — уже упомянутой индукции магнитного поля, суммарной силы тока колец, их площадью и углом между силовыми линиями и воображаемым перпендикуляром к кантилеверу. Если бы угол его наклона к силовым линиям был равен нулю, то никакого персистентного тока в кольцах не возникло бы, так как магнитный поток через кольца был бы равен нулю. Очевидно, что чем больше наклон кантилевера, тем больший ток течет по кольцам. Казалось бы, выгодно расположить пластину с кольцами перпендикулярно к силовым линиям, однако такая конфигурация создает нулевой вращательным момент кантилевера и не дает возможности измерить ток.
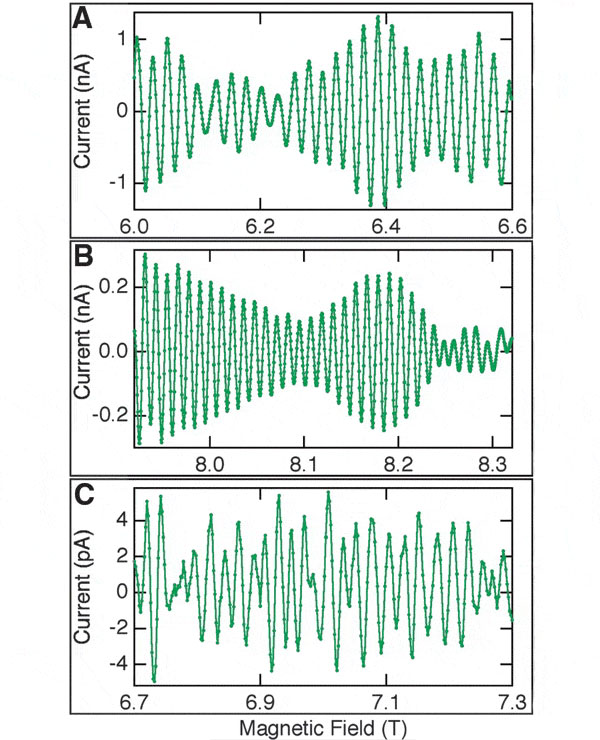
Кантилевер, как и любое другое тело, имеет характерную частоту свободных колебаний. Вращательный момент изменяет характерную частоту колебаний. Памятуя об этом и о том, что вращательный момент зависит также от силы тока в кольцах, авторы меняли индукцию магнитного поля и фиксировали лазером новую частоту свободных колебаний кантилевера. По отклонению частоты колебаний от первоначального значения ученые рассчитывали суммарный персистентный ток колец. Поскольку кольца в массиве совершенно одинаковые, то легко определить ток в единичном кольце. Результаты всех своих измерений ученые представили в виде графических зависимостей величины персистентного тока одного кольца от индукции магнитного поля (рис. 3) для разных углов наклона кремниевой пластины.
|
На каждой из кривых легко усматривается осциллирующий характер зависимости персистентного тока от индукции магнитного поля. Период осцилляций соответствует, как и предсказывает теория, магнитному потоку одного флюксоида, то есть 4,05·10–15 Тл·м2.
В заключение хотелось бы сказать об огромной — без преувеличения — важности статьи американских и немецких исследователей. Физики-теоретики наконец получили возможность сравнить свои модели с точными экспериментальными данными, выяснив заодно, какая из теорий персистентных токов наиболее правильно их описывает.