|
Сразу оговоримся, что далеко не каждый луч, испускаемый лазером, может переходить из одной фазы в другую. Для этого мощность устройства, генерирующего световой импульс, должна быть очень высокой — она должна превосходить некое пороговое значение, определяющееся характеристиками среды и длиной волны света. Например, для излучения с длиной волны 800 нм, распространяющегося в воздухе, этот порог — приблизительно 3 ГВт (1 гигаватт = 109 Вт). При таких условиях луч имеет настолько высокую интенсивность, что практически перестает быть подверженным дифракции и может оставаться сфокусированным и не расходящимся на протяжении нескольких десятков, а то и сотен метров.
Бездифракционное поведение лазерного луча объясняется эффектом Керра — изменением показателя преломления среды, через которую распространяется свет. Установлено, что разность между показателем преломления среды до движения через нее видимого излучения и после равна произведению его интенсивности на некоторый коэффициент пропорциональности. Для большинства веществ коэффициент пропорциональности больше нуля. Это означает, что распространение света вызывает увеличение показателя преломления среды. Но чтобы возникающую разность можно было детектировать, интенсивность света обязана быть очень большой.
Приведем наглядный пример. Для воздуха коэффициент пропорциональности равен 3 · 10–19 см2/Вт. Интенсивность солнечного света, согласно данным (PDF, 355 Кб) Всемирной метеорологической организации, равна 120 Вт/м2. Следовательно, свет от Солнца вызывает увеличение показателя преломления воздуха на ничтожно малую величину — 3,6 · 10–20%. И тем не менее, несмотря на такую очень и очень маленькую поправку, именно эффект Керра не позволяет лазерному лучу с интенсивностью больше вышеупомянутого порогового значения расходиться.
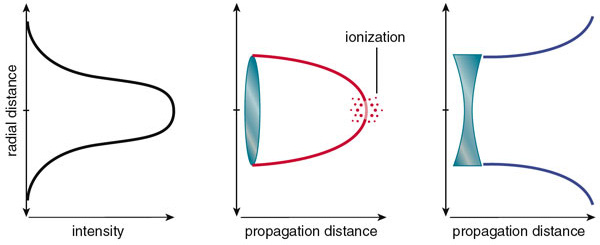
Каким образом эффект Керра помогает лазерному импульсу? Обычно интенсивность света на оси лазерного луча имеет максимум (рис. 1, слева) и симметрично уменьшается к границам. Предположим, что лазерный луч движется в воздухе. Тогда, согласно эффекту Керра, показатель преломления воздуха в середине луча окажется больше, чем на краях. Из-за этой оптической неоднородности воздушная среда формально ведет себя по отношению к лазерному излучению как собирающая линза: толщина луча уменьшается (рис. 1, центр), а интенсивность света увеличивается. То есть луч как бы сам себя фокусирует — происходит самофокусировка.
На первый взгляд кажется, что луч способен коллапсировать до нулевой толщины. Однако когда интенсивность света достигает некоторого значения, наступает многофотонная ионизация. Фотоны лазерного излучения выбивают электроны из молекул воздуха (молекул азота и кислорода). Освобожденные электроны формируют плазму. По сравнению с воздухом плазма обладает меньшим показателем преломления, поэтому она формально ведет себя как рассеивающая линза и начинает дефокусировать луч, уменьшая его интенсивность (рис. 1, справа). Проскочив область с плазмой, луч продолжает свое движение, и ситуация повторяется.
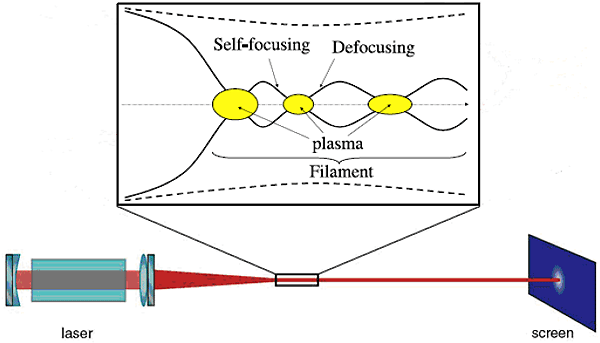
В итоге, балансируя между процессами самофокусировки и дефокусировки, луч, не расходясь, преодолевает расстояния в десятки и сотни метров (рис. 2).
|
Надо заметить, что помимо высокой интенсивности лазерный импульс должен обладать еще и маленькой продолжительностью — порядка фемтосекунды (10–15 секунды). В противном случае, вместо многофотонной ионизации среды, через которую он проходит, может возникнуть каскадная ионизация: концентрация освобожденных электронов становится такой, что они начинают ионизировать молекулы даже вдали от проходящего лазерного луча. Это приводит к дисбалансу между самофокусировкой и дефокусировкой. Луч перестает быть сфокусированным и быстро расходится.
То, что лазерный луч высокой интенсивности способен самофокусироваться и бездифракционным образом распространяться в среде, впервые экспериментально было продемонстрировано в 1994 году американскими физиками из Мичиганского университета при помощи 10-гигаваттного лазера, генерирующего импульсы длительностью 200 фемтосекунд с длиной волны 800 нм. В ходе этих экспериментов исследователи неожиданно обнаружили, что движение лазерного импульса в среде осуществляется в основном по очень тонким нитям, играющим для него роль своеобразных волноводов. Ученые назвали их филаментами (рис. 2), а сам процесс расщепления лазерного луча на нити-филаменты — филаментацией. На рис. 3 черные круглые области — это фотографии филаментов.
|
Между прочим, в настоящее время, когда появились очень мощные (тераваттные, 1012 Вт) лазерные установки, явление филаментации стало одним из наиболее активно изучаемых в теоретической и экспериментальной оптике.
Итак, сделаем промежуточный вывод: бездифракционное распространение лазерного луча высокой интенсивности возможно благодаря конкуренции двух процессов: самофокусировки луча, идущей из эффекта Керра, и дефокусировки, возникающей благодаря плазме. Казалось бы, на качественном уровне всё ясно. Однако в этом году в журнале Optics Express была опубликована статья Measurement of high order Kerr refractive index of major air components, в которой был подвергнут сомнению тот факт, что дефокусировка возникает благодаря плазме.
Французские ученые, авторы этой работы, провели серию экспериментов с тераваттными лазерными лучами, движущимися в различных газообразных средах: в воздухе, кислороде, аргоне и азоте. Было обнаружено, что начиная с интенсивности лазерного луча больше 26 ТВт/см2 показатель преломления никак не укладывается в ожидаемый линейный закон. Проще говоря, эффект Керра для очень больших значений интенсивности выглядит совершенно иначе. Изменение показателя преломления, по мнению авторов работы, нужно записывать не линейной зависимостью от интенсивности света, как это было раньше для эффекта Керра, а представлять в виде полинома четвертой степени, при этом коэффициенты, стоящие при нечетных степенях интенсивности, должны иметь положительные значения, а коэффициенты при четных степенях — отрицательные.
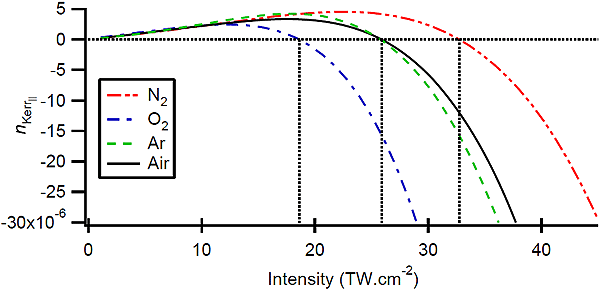
Как теперь, исходя из «нового» закона для эффекта Керра, трактовать бездифракционное распространение луча в среде, не привлекая влияние плазмы? Объяснение легко дать, если построить зависимость показателя преломления от интенсивности света (рис. 4).
|
Из графика видно, что, когда интенсивность достигает определенного значения для заданной среды, прибавка к показателю преломления становится отрицательной. Например, для воздуха это 26 ТВт/см2. В этот момент среда начинает вести себя как рассеивающая линза, дефокусирует луч и уменьшает его интенсивность. Далее картина повторяется. Выходит, что процессы самофокусировки и дефокусировки можно объяснить в рамках обновленного нелинейного эффекта Керра.
Основываясь на экспериментальных изысканиях своих французских коллег, испанские физики-теоретики решили по-новому взглянуть на распространение высокоинтенсивного лазерного луча, в частности на процесс филаментации. Они подставили в уравнение (нелинейное уравнение Шрёдингера), описывающее распространение световой волны в нелинейной среде, новую зависимость для показателя преломления в эффекте Керра, а затем численно решили его отдельно для кислородной и воздушной среды.
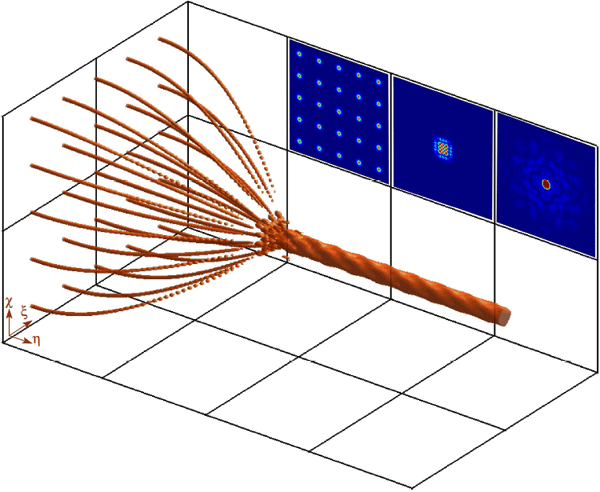
Оказалось, что, в зависимости от значения интенсивности, процесс филаментации имеет две фазы. Пока интенсивность лазерного луча не перешагнула некоторого критического значения, каждый филамент представляет собой цепочку локализованных в пространстве шарообразных областей (пузырьков) с максимумом интенсивности в их центрах и с плавным уменьшением до нуля на краях (рис. 5). Эти области образуют в профиле лазерного луча (в плоскости, перпендикулярной направлению его движения) регулярную упорядоченную решетку.
Чтобы исключить возможные спекуляции, заметим, что ни о какой смене квантовой статистики фотонов речи не идет (фотоны как были бозонами, так и остались). Авторы статьи рассчитали, что давление лазерного луча в этой фазе пропорционально квадрату его интенсивности. Если каждый пузырек вообразить фермионом (частица с полуцелым спином), а интенсивность луча представить как плотность этих пузырьков, то на выходе получим квадратичную зависимость давления от плотности, которая имеет место как раз для вырожденного газа фермионов. Используя эту аналогию, авторы и ввели в своей статье термин «фермионные пузырьки» и название для данной фазы — «фермионный свет».
|
Дальнейшее увеличение интенсивности лазерного луча (его можно достичь, например, поставив на пути лазерного луча специальную собирающую линзу) приводит к постепенному сближению цепочек фермионных пузырьков или филаментов. Когда интенсивность достигает критического значения (критическое значение для воздуха, согласно расчетам авторов, составляет около 30 ТВт/см2), пузырьки объединяются в один толстый филамент. В его пределах интенсивность света распределена равномерным образом (рис. 5) и резко падает до нуля за пределами филамента. Авторы рассчитали, что световое давление, которое оказывает новообразованная структура, обратно пропорционально ее радиусу. Поскольку формально полученная зависимость аналогична известной формуле Лапласа, определяющей добавочное давление жидкости в зависимости от кривизны ее поверхности, авторы назвали данную фазу лазерного луча жидкой каплей.
Таким образом, регулируя интенсивность лазерного луча, можно наблюдать фазовый переход из фермионного состояния в состояние жидкой капли и наоборот. Разумеется, переключение между фазами обнаружено пока что только «на бумаге». Однако авторы статьи надеются, что их теория вскоре будет проверена и поможет остальным ученым лучше понять процесс филаментации высокоинтенсивного лазерного луча. Кроме того, в заключении статьи исследователи говорят о том, что результаты их теоретических изысканий могут указать путь к улучшению эффективности экспериментов по конденсации водяного пара в атмосфере с помощью лазерных лучей (см.: Конденсировать водяной пар в атмосфере можно с помощью лазера, «Элементы», 23.06.2010).