|
Обычно, когда говорят о турбулентности, имеют в виду неупорядоченное, хаотическое движение среды — жидкости, газа, плазмы. Но в наши дни понятие «турбулентность» уже имеет более широкий смысл. Есть «привычная» турбулентность с вихрями, которую называют сильной турбулентностью, а есть волновая (или слабая) турбулентность. Этот второй вид неупорядоченного движения наблюдается, грубо говоря, там, где есть волны — это могут быть волны на поверхности океана во время шторма, альфвеновские волны в солнечной плазме (см. новость на «Элементах» В солнечной короне наконец обнаружены альфвеновские волны, 04.09.2007), спиновые волны в твердом теле, ленгмюровские волны. Существует даже оптическая турбулентность — связанная с распространением световых волн в сильно нелинейной среде.
Однако экспериментов по изучению волновой турбулентности очень мало, и большинство из них связано с изучением этого явления на поверхности жидкости, где волновую турбулентность можно условно разделить на два вида — капиллярную и гравитационную. Капиллярную турбулентность (когда длина волн на поверхности жидкости мала и их появление связано с поверхностным натяжением) уже наблюдали с помощью оптических методов. Гравитационную же турбулентность, имеющую место для волн большей длины, когда уже становятся существенными эффекты силы тяжести, можно изучать только методами in situ — то есть на месте, в режиме реального времени, следить за поведением волн на поверхности океана, моря или больших водоемов.
В 2007 году в журнале Physical Review Letters была опубликована статья французских исследователей Observation of Gravity-Capillary Wave Turbulence (в открытом доступе с ней можно ознакомиться здесь), в которой экспериментально исследовался переход из режима капиллярной волновой турбулентности в гравитационную на поверхности ртути.
На это раз физики из Франции усложнили свою задачу, замахнувшись на изучение волновой турбулентности на поверхности не обычной, а магнитной жидкости — так называемой феррожидкости. Полный текст их статьи Wave Turbulence on the Surface of a Ferrofluid in a Magnetic Field, опубликованной в Physical Review Letters, доступен в виде препринта.
Что же представляет собой феррожидкость? По своим магнитным свойствам жидкости делятся на диамагнетики, ослабляющие магнитное поле, и парамагнетики, которые это поле усиливают. Но только усиливают они его очень и очень незначительно. Своеобразным рекордсменом по увеличению индукции магнитного поля следует считать такую экзотическую жидкость, как сжиженный кислород при температуре 90 К — он усиливает внешнее магнитное поле в 1,0034 раза. Как видим, это усиление всё равно чрезвычайно мало — настоящих ферромагнетиков, усиливающих магнитное поле во много раз, среди жидкостей нет. Тем не менее получить жидкую среду с почти ферромагнитными свойствами реально. Для этого достаточно в обычную жидкость накрошить очень мелкие частицы ферромагнетика (размером порядка нанометра и с концентрацией 1016–1018 частиц на 1 см3). Получившуюся смесь и назвали феррожидкостью. Благодаря малым размерам взвешенных частиц и мерам, предотвращающим их слипание, магнитные жидкости демонстрируют высокую стабильность, практически не разлагаясь, и после того, как магнитное поле убрано, восстанавливают свои прежние свойства.
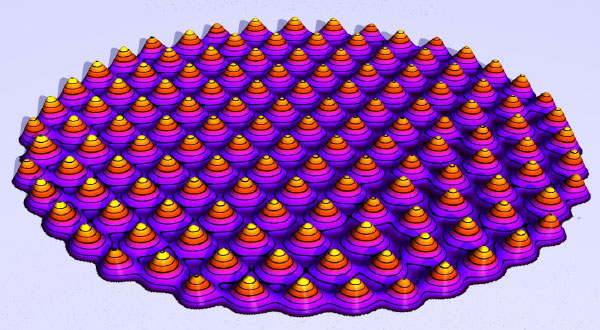
Самые удивительные свойства феррожидкости проявляются, когда к ней начинают прикладывать внешнее магнитное поле, направленное перпендикулярно к ее поверхности. Тогда получается, что поверхность феррожидкости формируется не только под воздействием силы тяжести и силы поверхностного натяжения, как обычная жидкость, но еще и под воздействием магнитной силы. По мере увеличения индукции магнитного поля на поверхности феррожидкости начинает образовываться рябь, а затем, когда магнитное поле достигло некого критического значения Bc, возникают неподвижные пики — или, говоря научным языком, правильная гексагональная решетка из вершин застывших волн (см. рис. 1). Такая структура нестабильна и носит название «неустойчивость Розенцвейга», по имени ученого, который первым ее наблюдал.
Вообще говоря, при определенных условиях неустойчивость Розенцвейга можно превратить в целое искусство, создавая на поверхности феррожидкости самые замысловатые фигуры и даже скульптуры (см. видео).
Также, справедливости ради скажем, что название для такого вида жидкости было выбрано не очень удачно, поскольку, в отличие от ферромагнетика, никакой остаточной намагниченности при снятии внешнего магнитного поля, так же как и спонтанной намагниченности, в феррожидкости не наблюдается. Если не прикладывать магнитное поле, то перед нами будет находиться самая обычная жидкость с взвешенными в ней частицами ферромагнетика.
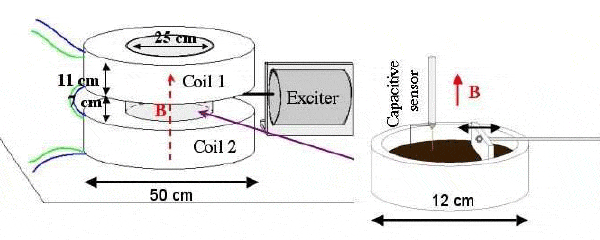
Так вот, французские ученые были первыми, кто наблюдал и изучал волновую турбулентность на поверхности феррожидкости. Схема их экспериментальной установки показана на рис. 2.
|
Установка состоит из цилиндрического контейнера (внутренний диаметр 12 см, высота 4 см), заполненного на глубину 2 см феррожидкостью, представляющей собой раствор с частицами оксида железа размером приблизительно 7,6 нм. Контейнер помещается в пространство между двумя катушками (зазор между катушками равен 7 см). Протекающий по катушкам постоянный ток генерирует магнитное поле между ними с максимальным значением индукции 0,078 Тл. Чтобы иметь возможность наблюдать волновую турбулентность в феррожидкости, ученые подвели к контейнеру возбудитель колебаний, который создавал низкочастотные (1–5 Гц) случайные «встряски» на поверхности жидкости. Амплитуда ? возникающих турбулентных волн в феррожидкости фиксировалась с помощью специально прокалиброванного конденсатора. Измерения показали, что неустойчивость Розенцвейга (образование стационарных пиков на поверхности) для такой феррожидкости наступает при значении индукции магнитного поля около 0,0294 ± 0,0002 Тл, и прекрасно согласовывается с теоретическими предсказаниями (0,02923 Тл).
Несколько слов о методике исследования. Поскольку волновые процессы на поверхности феррожидкости являются хаотическими (турбулентными), фиксировать изменяющиеся случайным образом амплитуды ? рождающихся волн при заданном значении индукции магнитного поля и в дальнейшем их визуализировать в виде графика функции ?(t), сложно и неудобно для дальнейшего анализа. Поэтому при изучении случайных процессов (это касается исследования не только волновой турбулентности, но и турбулентности вообще) ученые прибегают к спектральному анализу. Функцию ?(t) от времени возводят в квадрат и трансформируют с помощью Фурье-преобразования в функцию, называемую спектральной плотностью мощности «сигнала» (в данном случае сигнал — это волновой процесс на поверхности феррожидкости) и зависящую от обратного времени или от частоты.
Для чего это делается? Поясним на примере уже упоминавшейся статьи 2007 года Observation of Gravity-Capillary Wave Turbulence. Экспериментальная установка, которая использовалась французами в более ранней работе, идентична установке в обсуждаемом здесь исследовании. На рис. 3 слева приведен график зависимости амплитуды рождающихся турбулентных волн ?(t) в обычной (не магнитной) жидкости.
График не очень информативный и, как говорят физики, «шумящий», что, в принципе, неудивительно для случайного процесса. Но чтобы точно удостовериться, что данный процесс истинно случайный и хаотический, необходимо визуализировать спектральную плотность мощности функции ?(t), то есть зависимость амплитуды поверхностных волн от времени. Если график этой функции не будет иметь явно выделенных пиков, то процесс действительно случайный. График на рис. 3 справа показывает, что образующиеся поверхностные волны действительно являются волновой турбулентностью, так как явных всплесков на графике не наблюдается. Правда, одна особенность — изгиб на частоте 17 Гц — на приведенном графике спектральной плотности мощности есть, однако эта особенность связана с переходом (кроссовером) от режима гравитационной волновой турбулентности к капиллярной.
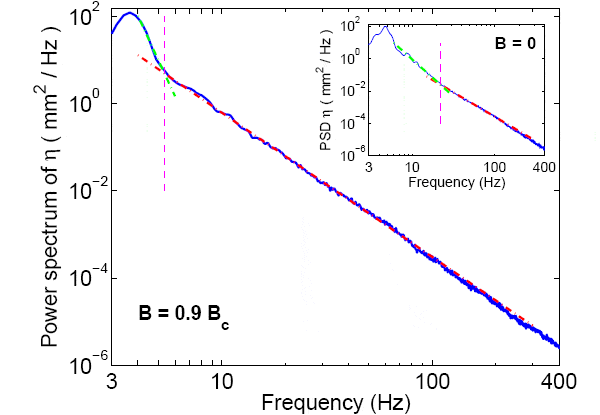
Такой же анализ был проведен французскими учеными и для феррожидкости в присутствии магнитного поля: спектральная плотность мощности сигнала — функции зависимости образующихся волн от времени — приведена на рис. 4. На вставке показана та же зависимость, но уже в отсутствие внешнего поля (график подобен графику на рис. 3 справа).
|
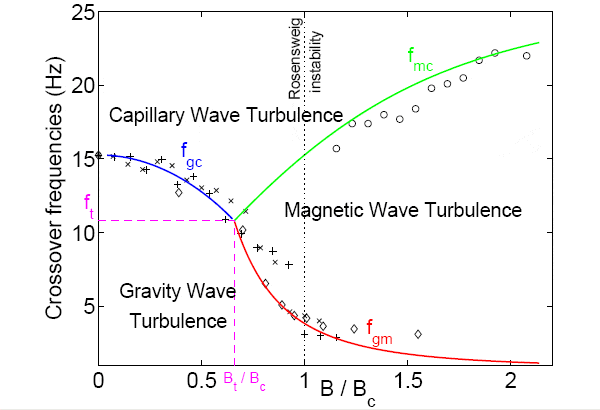
Пожалуй, главным результатом исследователей стал график эволюции режимов волновой турбулентности в феррожидкости при возрастании индукции внешнего магнитного поля (см. рис. 5) в различных частотных диапазонах функции спектральной плотности мощности. Нетрудно увидеть, что по сравнению с обычной жидкостью (см. рис. 3 справа) на графике появилась новая область — режим магнитной волновой турбулентности. Особенно он (режим) заметен, когда индукция внешнего магнитного поля перешагнула порог неустойчивости Розенцвейга (на рис. 5 — точечная линия, перпендикулярная оси абсцисс). Уточним еще раз на всякий случай, что речь здесь идет не о частоте возбудителя колебаний (у него она изменялась от 1 до 6 Гц), а о частоте, относящейся к функции спектральной плотности мощности волнового процесса на поверхности феррожидкости.
|
Результаты исследований, представленные в виде графика на рис. 5, можно пояснить так. При очень малых значениях индукции магнитного поля в области малых частот доминирующим процессом на поверхности феррожидкости является гравитационная волновая турбулентность, соответственно при больших частотах — капиллярная. Проще говоря, когда поле слабое, феррожидкость ничем не отличается от жидкости обычной. Магнитная волновая турбулентность начинает проявляться, когда магнитное поле достигнет некоторого значения Bt (для данной феррожидкости Bt = 0,65Bc, где Bc — индукция магнитного поля неустойчивости Розенцвейга) и в зависимости от частотного диапазона можно даже говорить либо о магнито-гравитационной турбулентности (малые частоты), либо о магнито-капиллярной в диапазоне высоких частот.
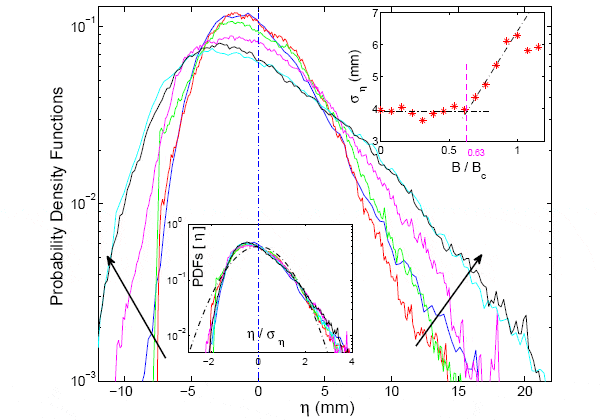
Ну и напоследок авторы приводят график распределения амплитуды «гуляющих» по поверхности феррожидкости волн (рис. 6) для разных значений индукции магнитного поля.
|
Большинство образующихся турбулентных волн имеют амплитуду от –5 до 5 мм (знак минус означает впадины на поверхности магнитной жидкости). Однако в поле, превышающем поле неустойчивости Розенцвейга, существует вероятность наблюдать волну с амплитудой 2 см.